RNN部分问题的原理解释

1. RNN的前向传播原理

以一个Many-to-Many的简单RNN为例(输入输出维度相等)：

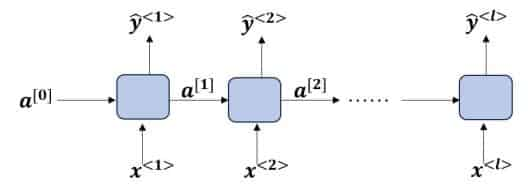
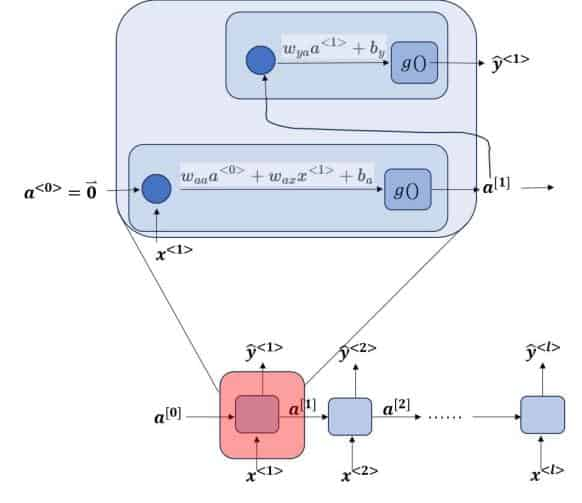
每一时间单位的前向计算过程为：

第一步也可以简写为：

也记作.

有的RNN论文中还会把第一步的激活函数放到里面，即写作：

这两个公式在宏观意义上被认为是等价的。

2. RNN的损失函数与反向传播(Back Propagation Through Time, BPTT)

现在，通过上一步已经能够找到预测值，在真实值已知的条件下，单步的损失可以借助交叉熵定义为：(当然也可以用残差定义)

模型总的损失函数为：(取时间平均，某些论文也没有做时间平均，个人感觉时间平均没有太大的必要)

优化目标为：

分析可知，优化的目标函数与四个参量有关：。因此，计算损失函数相对于这四者的偏导数，不断进行参数更新，直到模型收敛，就是求解BRTT的大致过程。

为便于分析，不考虑偏置项对模型收敛的影响，只考虑权重矩阵。首先分析: 是一个与输出的预测值相关的值，因此根据链式法则有：

分两项考虑，第一项：

第二项：

其次分析:

在上式中，第一项和第二项不需要循环计算，而第三项是需要不断地计算每一步参数对的影响。

观察上面的递归式，不难发现有以下的结构规律，对于，设,为一个序列：

下面把,分别替换成,,

最终算式为

3. RNN的时序记忆能力短的原因？

为便于分析，假设隐藏层的激活函数为线性激活函数（也可以说没有激活），将RNN的前馈输出展开：

不难看出，每一次的前向传播都会对之前的激活值产生影响，一旦序列较长，模型对于附近的值的敏感程度就明显高于之前的输入，RNN表现出了“遗忘”的现象。

4. RNN的梯度爆炸与梯度消失成因？

假定我们使足够简单的线性激活函数作为隐藏层的激活函数,（或者说不适用任何激活函数）根本原因在求解时，出现了：

即

假定可对角化，令的n个特征值为{, 且满足。其对应的特征向量为，他们组成向量基。则在这个向量空间下:

且有(待求证？)：

如果有满足

因为, . 由此我们可以看出，随着的增大而指数级增大，且是沿着的方向增长。

虽然上面的证明可以对角化，但是如果用Jordan正则表达式，上面的证明可以扩展到不仅仅是最大特征值的特征向量，而且可以考虑共享相同最大特征值的特征向量所跨越的整个子空间，扩展到更广泛的情况。（这一步尚且还没有读懂 ~~（恶补矩阵论去了）~~ ）

于是我们能够得出梯度爆炸或梯度消失的充分条件：

梯度爆炸的充分条件：$t $时，$ _1 $（$ $的所有特征值中最大的）$ $。

梯度消失的充分条件：$t $时，$ _1 $（$ $的所有特征值中最大的）$ $。

以上讨论的都是基于激活函数是线性的（即没有使用任何激活函数）。如果是针对非线性函数，则有非线性函数的输出一定有界这一特性，即：

证明：只要, 其中是权重矩阵中的最大特征值，就足以发生梯度消失问题

于是,满足

因为, 根据上式，模型非常深的时候（很大），梯度指数下降至0值附近。

根据梯度消失的证明思路，我们也很容易得到梯度爆炸的条件：

从微分方程到RNN

令是-维状态，考虑一个一般的非线性一阶非均质常微分方程，描述状态信号随时间的变化。(这很像状态估计问题)

状态随时间变化可以认为有两部分在作用，其中前者与输入（或者引用状态估计问题中的说法：观测）有关:

于是，一个在物理、化学、工程领域非常常见的方程式就出现了：（至少原作者Sherstinsky是这么说的）

除此之外，还有其他形式，比如脑动力学研究中的加性模型（Addictive Model）：

加性模型的三个时间向量如下定义：

式中，是状态的变换，为非线性激活函数。状态随时间的变化就可以展开写成如下形式：

该方程是一个具有离散延迟的非线性常延迟微分方程 (DDE)。首项是

5. LSTM的前向传播

在LSTM（以及GRU）中，我们要引入一个新概念：候选记忆元（candidate memory cell）,用表示，在每一个步长里，用候选值重写之前记忆的值。（这里的c和传统RNN中的隐藏层激活值a从本质上来说是同一个表达）。为了应对RNN的"遗忘问题"，LSTM采取的策略是（核心思想）建立一些门函数，其中一个门用来从单元中输出条目，我们将其称为输出门（output gate,）。另外一个门用来决定何时将数据读入单元，我们将其称为输入门/更新门（input/update gate,）。我们还需要一种机制来重置单元的内容，由遗忘门（forget gate, ） 来管理。

6. LSTM中的BPTT：

基于, 可以得到每一步的预测值：

单步损失$^{}({}, y^{}) $略去，（与上文的传统RNN一样），模型总损失为：

优化目标为：

为了便于讨论，依然忽略偏置值对模型的影响，着重考虑权重矩阵。

首先是损失函数关于的导数

公式之所以会分为五项，是因为在反向传播过程中存在两个“分岔路口”。，再往下求解之前一个时刻，则公式内部的继续展开为五项。

求解的影响的思路和类似，同样存在五项；求解前一时刻的的影响则会分别出现4条链路（4项）。对于的影响的求解就较为简单，因为不需要之前时刻的信息。

LSTM的时序记忆能力强的原因？

LSTM的核心是前向传播中的记忆单元，通过模型学习，调节三个门函数的权重矩阵的值，有可能会产生,从而有

因为有记忆单元的存在，LSTM能实现在较长的时间内“记住”之前的信息。

LSTM对BPTT的梯度爆炸和梯度消失的缓解

LSTM对梯度消失的缓解依然是在更新记忆单元。反向传播的过程中涉及计算,将其展开能够得到：

在LSTM迭代过程中，针对而言，模型在学习的过程中，有了三个门函数的权重矩阵，每一步可以通过更改权重矩阵去自主选择在[0,1]之间，或者大于1，整体也就不会一直减小，远距离梯度不至于完全消失，也就能够解决RNN中存在的梯度消失问题。

LSTM和ResNet中的残差逼近思想有些相似，通过构建从前一时刻记忆单元到下一时刻记忆单元的“短路连接”，使梯度得已有效地反向传播，以应对梯度消失。

至于梯度爆炸问题，LSTM的提出不能说完全规避，从RNN的单项式连乘到LSTM的多项式连乘，后者还有相加运算，有可能梯度值大于1。毕竟LSTM的提出主要是为了缓解梯度消失的问题。